IMO Shortlist 1968 problem 15
Dodao/la:
arhiva2. travnja 2012. Let

be a natural number. Prove that
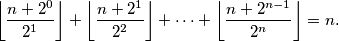
For any real number

, the number
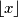
represents the largest integer smaller or equal with

.
%V0
Let $n$ be a natural number. Prove that $$\left\lfloor \frac{n+2^0}{2^1} \right\rfloor + \left\lfloor \frac{n+2^1}{2^2} \right\rfloor + \cdots + \left\lfloor \frac{n+2^{n-1}}{2^n} \right\rfloor = n\text{.}$$
For any real number $x$, the number $\lfloor x \rfloor$ represents the largest integer smaller or equal with $x$.
Izvor: Međunarodna matematička olimpijada, shortlist 1968