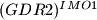
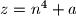
Prove that there exist infinitely many natural numbers with the following property: The number is not prime for any natural number
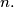
%V0
$(GDR 2)^{IMO1}$ Prove that there exist infinitely many natural numbers $a$ with the following property: The number $z = n^4 + a$ is not prime for any natural number $n.$
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
Prove that there exist infinitely many natural numbers 
with the following property: The number 
is not prime for any natural number 