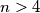
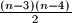
Given points in the plane, no three collinear. Prove that there are at least convex quadrilaterals with vertices amongst the points.
%V0
Given $n>4$ points in the plane, no three collinear. Prove that there are at least $(n-3)(n-4)\over2$ convex quadrilaterals with vertices amongst the $n$ points.
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
points in the plane, no three collinear. Prove that there are at least 
convex quadrilaterals with vertices amongst the 
points.