IMO Shortlist 1969 problem 47
Dodao/la:
arhiva2. travnja 2012. 
is a point on the semicircle diameter

, between

and

.

is the foot of the perpendicular from

to

. The circle
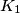
is the incircle of

, the circle
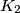
touches
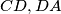
and the semicircle, the circle
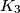
touches
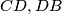
and the semicircle. Prove that
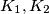
and
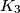
have another common tangent apart from

.
%V0
$C$ is a point on the semicircle diameter $AB$, between $A$ and $B$. $D$ is the foot of the perpendicular from $C$ to $AB$. The circle $K_1$ is the incircle of $ABC$, the circle $K_2$ touches $CD,DA$ and the semicircle, the circle $K_3$ touches $CD,DB$ and the semicircle. Prove that $K_1,K_2$ and $K_3$ have another common tangent apart from $AB$.
Izvor: Međunarodna matematička olimpijada, shortlist 1969