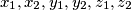
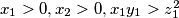
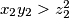
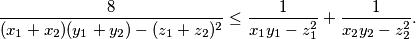
Given real numbers satisfying , and , prove that: Give necessary and sufficient conditions for equality.
%V0
Given real numbers $x_1,x_2,y_1,y_2,z_1,z_2$ satisfying $x_1>0,x_2>0,x_1y_1>z_1^2$, and $x_2y_2>z_2^2$, prove that: $${8\over(x_1+x_2)(y_1+y_2)-(z_1+z_2)^2}\le{1\over x_1y_1-z_1^2}+{1\over x_2y_2-z_2^2}.$$ Give necessary and sufficient conditions for equality.
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
satisfying 
, and 
, prove that: 
Give necessary and sufficient conditions for equality.