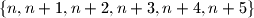
Find all positive integers such that the set can be partitioned into two subsets so that the product of the numbers in each subset is equal.
%V0
Find all positive integers $n$ such that the set $\{n,n+1,n+2,n+3,n+4,n+5\}$ can be partitioned into two subsets so that the product of the numbers in each subset is equal.
Izvor: Međunarodna matematička olimpijada, shortlist 1970
Školjka 
such that the set 
can be partitioned into two subsets so that the product of the numbers in each subset is equal.