IMO Shortlist 1971 problem 5
Dodao/la:
arhiva2. travnja 2012. Let
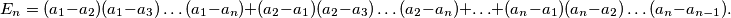
Let
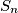
be the proposition that
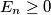
for all real
. Prove that
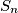
is true for
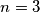
and
, but for no other
.
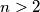
%V0
Let $$E_n=(a_1-a_2)(a_1-a_3)\ldots(a_1-a_n)+(a_2-a_1)(a_2-a_3)\ldots(a_2-a_n)+\ldots+(a_n-a_1)(a_n-a_2)\ldots(a_n-a_{n-1}).$$ Let $S_n$ be the proposition that $E_n\ge0$ for all real $a_i$. Prove that $S_n$ is true for $n=3$ and $5$, but for no other $n>2$.
Izvor: Međunarodna matematička olimpijada, shortlist 1971
Školjka 
