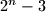
Prove that we can find an infinite set of positive integers of the from (where is a positive integer) every pair of which are relatively prime.
%V0
Prove that we can find an infinite set of positive integers of the from $2^n-3$ (where $n$ is a positive integer) every pair of which are relatively prime.
Izvor: Međunarodna matematička olimpijada, shortlist 1971
Školjka 
(where 
is a positive integer) every pair of which are relatively prime.