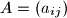
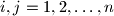
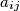
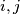
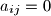
Let , where , be a square matrix with all non-negative integers. For each such that , the sum of the elements in the th row and the th column is at least . Prove that the sum of all the elements in the matrix is at least .
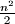
%V0
Let $A = (a_{ij})$, where $i,j = 1,2,\ldots,n$, be a square matrix with all $a_{ij}$ non-negative integers. For each $i,j$ such that $a_{ij} = 0$, the sum of the elements in the $i$th row and the $j$th column is at least $n$. Prove that the sum of all the elements in the matrix is at least $\frac {n^2}{2}$.
Izvor: Međunarodna matematička olimpijada, shortlist 1971
Školjka 
, where 
, be a square matrix with all 
non-negative integers. For each 
such that 
, the sum of the elements in the 
th row and the 
th column is at least 
. Prove that the sum of all the elements in the matrix is at least 
.