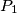
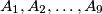
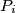
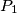
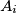
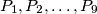
Let be a convex polyhedron with vertices . Let be the polyhedron obtained from by a translation that moves to . Prove that at least two of the polyhedra have an interior point in common.
%V0
Let $P_1$ be a convex polyhedron with vertices $A_1,A_2,\ldots,A_9$. Let $P_i$ be the polyhedron obtained from $P_1$ by a translation that moves $A_1$ to $A_i$. Prove that at least two of the polyhedra $P_1,P_2,\ldots,P_9$ have an interior point in common.
Izvor: Međunarodna matematička olimpijada, shortlist 1971
Školjka 
be a convex polyhedron with vertices 
. Let 
be the polyhedron obtained from 
to 
. Prove that at least two of the polyhedra 
have an interior point in common.