Prove the following assertion: The four altitudes of a tetrahedron intersect in a point if and only if
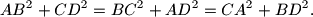
%V0
Prove the following assertion: The four altitudes of a tetrahedron $ABCD$ intersect in a point if and only if
$$AB^2 + CD^2 = BC^2 + AD^2 = CA^2 + BD^2.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1972
Školjka 
intersect in a point if and only if