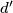
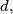
Establish if there exists a finite set of points in space, not all situated in the same plane, so that for any straight line which contains at least two points from M there exists another straight line , parallel with but distinct from , which also contains at least two points from .
%V0
Establish if there exists a finite set $M$ of points in space, not all situated in the same plane, so that for any straight line $d$ which contains at least two points from M there exists another straight line $d'$, parallel with $d,$ but distinct from $d$, which also contains at least two points from $M$.
Izvor: Međunarodna matematička olimpijada, shortlist 1973
Školjka 
of points in space, not all situated in the same plane, so that for any straight line 
which contains at least two points from M there exists another straight line 
, parallel with 
but distinct from