IMO Shortlist 1973 problem 10
Dodao/la:
arhiva2. travnja 2012. Let
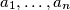
be

positive numbers and
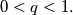
Determine

positive numbers
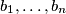
so that:
a.)
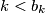
for all
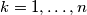
,
b.)
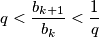
for all
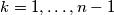
,
c.)
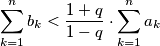
.
%V0
Let $a_1, \ldots, a_n$ be $n$ positive numbers and $0 < q < 1.$ Determine $n$ positive numbers $b_1, \ldots, b_n$ so that:
a.) $k < b_k$ for all $k = 1, \ldots, n$ ,
b.) $\displaystyle q < \frac{b_{k+1}}{b_{k}} < \frac{1}{q}$ for all $k = 1, \ldots, n-1$,
c.) $\displaystyle \sum \limits^n_{k=1} b_k < \frac{1+q}{1-q} \cdot \sum \limits^n_{k=1} a_k$.
Izvor: Međunarodna matematička olimpijada, shortlist 1973