IMO Shortlist 1973 problem 17
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 is a set of non-constant functions
is a set of non-constant functions  . Each
. Each  is defined on the real line and has the form
is defined on the real line and has the form 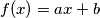 for some real
for some real 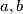 . If
. If  and
and  are in
are in  , then so is
, then so is 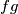 , where
, where 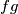 is defined by
is defined by 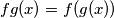 . If
. If  is in
is in  , then so is the inverse
, then so is the inverse 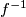 . If
. If 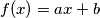 , then
, then 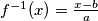 . Every
. Every  in
in  has a fixed point (in other words we can find
has a fixed point (in other words we can find 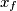 such that
such that 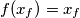 . Prove that all the functions in
. Prove that all the functions in  have a common fixed point.
have a common fixed point. Izvor: Međunarodna matematička olimpijada, shortlist 1973
 Školjka
Školjka 
