IMO Shortlist 1974 problem 1
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Three players 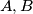 and
and  play a game with three cards and on each of these
play a game with three cards and on each of these  cards it is written a positive integer, all
cards it is written a positive integer, all  numbers are different. A game consists of shuffling the cards, giving each player a card and each player is attributed a number of points equal to the number written on the card and then they give the cards back. After a number
numbers are different. A game consists of shuffling the cards, giving each player a card and each player is attributed a number of points equal to the number written on the card and then they give the cards back. After a number 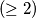 of games we find out that A has
of games we find out that A has 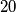 points,
points,  has
has 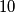 points and
points and  has
has 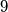 points. We also know that in the last game B had the card with the biggest number. Who had in the first game the card with the second value (this means the middle card concerning its value).
points. We also know that in the last game B had the card with the biggest number. Who had in the first game the card with the second value (this means the middle card concerning its value).
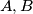 and
and  play a game with three cards and on each of these
play a game with three cards and on each of these  cards it is written a positive integer, all
cards it is written a positive integer, all  numbers are different. A game consists of shuffling the cards, giving each player a card and each player is attributed a number of points equal to the number written on the card and then they give the cards back. After a number
numbers are different. A game consists of shuffling the cards, giving each player a card and each player is attributed a number of points equal to the number written on the card and then they give the cards back. After a number 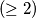 of games we find out that A has
of games we find out that A has 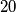 points,
points,  has
has 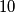 points and
points and  has
has 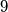 points. We also know that in the last game B had the card with the biggest number. Who had in the first game the card with the second value (this means the middle card concerning its value).
points. We also know that in the last game B had the card with the biggest number. Who had in the first game the card with the second value (this means the middle card concerning its value). Izvor: Međunarodna matematička olimpijada, shortlist 1974
 Školjka
Školjka 
