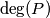
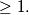
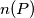
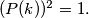
Let be a polynomial with integer coefficients. We denote its degree which is Let be the number of all the integers for which we have Prove that
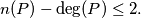
%V0
Let $P(x)$ be a polynomial with integer coefficients. We denote $\deg(P)$ its degree which is $\geq 1.$ Let $n(P)$ be the number of all the integers $k$ for which we have $(P(k))^{2}=1.$ Prove that $n(P)- \deg(P) \leq 2.$
Izvor: Međunarodna matematička olimpijada, shortlist 1974
Školjka 
be a polynomial with integer coefficients. We denote 
its degree which is 
Let 
be the number of all the integers 
for which we have 
Prove that 