IMO Shortlist 1975 problem 8
Dodao/la:
arhiva2. travnja 2012. In the plane of a triangle
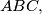
in its exterior
we draw the triangles
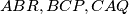
so that
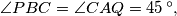
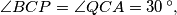
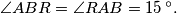
Prove that
a.)
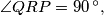
and
b.)
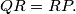
%V0
In the plane of a triangle $ABC,$ in its exterior$,$ we draw the triangles $ABR, BCP, CAQ$ so that $\angle PBC = \angle CAQ = 45\,^{\circ},$ $\angle BCP = \angle QCA = 30\,^{\circ},$ $\angle ABR = \angle RAB = 15\,^{\circ}.$
Prove that
a.) $\angle QRP = 90\,^{\circ},$ and
b.) $QR = RP.$
Izvor: Međunarodna matematička olimpijada, shortlist 1975
Školjka 
