IMO Shortlist 1975 problem 10
Dodao/la:
arhiva2. travnja 2012. Determine the polynomials P of two variables so that:
a.) for any real numbers
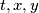
we have
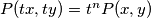
where

is a positive integer, the same for all
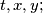
b.) for any real numbers

we have
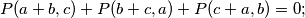
c.)
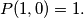
%V0
Determine the polynomials P of two variables so that:
a.) for any real numbers $t,x,y$ we have $P(tx,ty) = t^n P(x,y)$ where $n$ is a positive integer, the same for all $t,x,y;$
b.) for any real numbers $a,b,c$ we have $P(a + b,c) + P(b + c,a) + P(c + a,b) = 0;$
c.) $P(1,0) =1.$
Izvor: Međunarodna matematička olimpijada, shortlist 1975