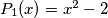
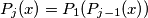
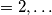
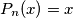
Let and for j Prove that for any positive integer n the roots of the equation are all real and distinct.
%V0
Let $P_{1}(x)=x^{2}-2$ and $P_{j}(x)=P_{1}(P_{j-1}(x))$ for j$=2,\ldots$ Prove that for any positive integer n the roots of the equation $P_{n}(x)=x$ are all real and distinct.
Izvor: Međunarodna matematička olimpijada, shortlist 1976
Školjka 
and 
for j
Prove that for any positive integer n the roots of the equation 
are all real and distinct.