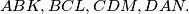
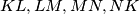
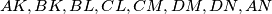
In the interior of a square we construct the equilateral triangles Prove that the midpoints of the four segments and the midpoints of the eight segments are the 12 vertices of a regular dodecagon.
%V0
In the interior of a square $ABCD$ we construct the equilateral triangles $ABK, BCL, CDM, DAN.$ Prove that the midpoints of the four segments $KL, LM, MN, NK$ and the midpoints of the eight segments $AK, BK, BL, CL, CM, DM, DN, AN$ are the 12 vertices of a regular dodecagon.
Izvor: Međunarodna matematička olimpijada, shortlist 1977
Školjka 
we construct the equilateral triangles 
Prove that the midpoints of the four segments 
and the midpoints of the eight segments 
are the 12 vertices of a regular dodecagon.