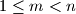
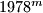
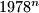
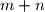
Let and be positive integers such that . In their decimal representations, the last three digits of are equal, respectively, so the last three digits of . Find and such that has its least value.
%V0
Let $m$ and $n$ be positive integers such that $1 \le m < n$. In their decimal representations, the last three digits of $1978^m$ are equal, respectively, so the last three digits of $1978^n$. Find $m$ and $n$ such that $m + n$ has its least value.
Izvor: Međunarodna matematička olimpijada, shortlist 1978
Školjka 
and 
be positive integers such that 
. In their decimal representations, the last three digits of 
are equal, respectively, so the last three digits of 
. Find 
has its least value.