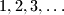
Let be an injective function from in itself. Prove that for any we have:
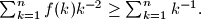
%V0
Let $f$ be an injective function from ${1,2,3,\ldots}$ in itself. Prove that for any $n$ we have: $\sum_{k=1}^{n} f(k)k^{-2} \geq \sum_{k=1}^{n} k^{-1}.$
Izvor: Međunarodna matematička olimpijada, shortlist 1978
Školjka 
be an injective function from 
in itself. Prove that for any 
we have: 