IMO Shortlist 1979 problem 4
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 We consider a prism which has the upper and inferior basis the pentagons: 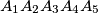 and
and 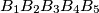 . Each of the sides of the two pentagons and the segments
. Each of the sides of the two pentagons and the segments 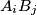 with
with 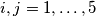 is colored in red or blue. In every triangle which has all sides colored there exists one red side and one blue side. Prove that all the 10 sides of the two basis are colored in the same color.
is colored in red or blue. In every triangle which has all sides colored there exists one red side and one blue side. Prove that all the 10 sides of the two basis are colored in the same color.
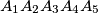 and
and 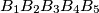 . Each of the sides of the two pentagons and the segments
. Each of the sides of the two pentagons and the segments 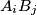 with
with 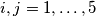 is colored in red or blue. In every triangle which has all sides colored there exists one red side and one blue side. Prove that all the 10 sides of the two basis are colored in the same color.
is colored in red or blue. In every triangle which has all sides colored there exists one red side and one blue side. Prove that all the 10 sides of the two basis are colored in the same color. Izvor: Međunarodna matematička olimpijada, shortlist 1979
 Školjka
Školjka 
