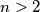
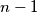
a.) For which is there a set of consecutive positive integers such that the largest number in the set is a divisor of the least common multiple of the remaining numbers?
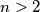
b.) For which is there exactly one set having this property?
%V0
a.) For which $n>2$ is there a set of $n$ consecutive positive integers such that the largest number in the set is a divisor of the least common multiple of the remaining $n-1$ numbers?
b.) For which $n>2$ is there exactly one set having this property?
Izvor: Međunarodna matematička olimpijada, shortlist 1981
Školjka 
is there a set of 
consecutive positive integers such that the largest number in the set is a divisor of the least common multiple of the remaining 
numbers?