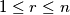
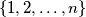
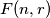
Take such that , and consider all subsets of elements of the set . Each subset has a smallest element. Let be the arithmetic mean of these smallest elements. Prove that:
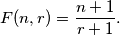
%V0
Take $r$ such that $1\le r\le n$, and consider all subsets of $r$ elements of the set $\{1,2,\ldots,n\}$. Each subset has a smallest element. Let $F(n,r)$ be the arithmetic mean of these smallest elements. Prove that: $$F(n,r)={n+1\over r+1}.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1981
Školjka 
such that 
, and consider all subsets of 
. Each subset has a smallest element. Let 
be the arithmetic mean of these smallest elements. Prove that: 