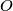
Three circles of equal radius have a common point and lie inside a given triangle. Each circle touches a pair of sides of the triangle. Prove that the incenter and the circumcenter of the triangle are collinear with the point .
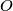
%V0
Three circles of equal radius have a common point $O$ and lie inside a given triangle. Each circle touches a pair of sides of the triangle. Prove that the incenter and the circumcenter of the triangle are collinear with the point $O$.
Izvor: Međunarodna matematička olimpijada, shortlist 1981
Školjka 
and lie inside a given triangle. Each circle touches a pair of sides of the triangle. Prove that the incenter and the circumcenter of the triangle are collinear with the point