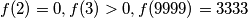
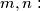
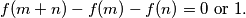
The function is defined on the positive integers and takes non-negative integer values. and for all Determine .
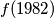
%V0
The function $f(n)$ is defined on the positive integers and takes non-negative integer values. $f(2)=0,f(3)>0,f(9999)=3333$ and for all $m,n:$ $$f(m+n)-f(m)-f(n)=0 \text{ or } 1.$$ Determine $f(1982)$.
Izvor: Međunarodna matematička olimpijada, shortlist 1982
Školjka 
is defined on the positive integers and takes non-negative integer values. 
and for all 
Determine 
.