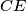
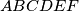
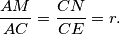
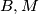
The diagonals and of the regular hexagon are divided by inner points and respectively, so that Determine if and are collinear.
%V0
The diagonals $AC$ and $CE$ of the regular hexagon $ABCDEF$ are divided by inner points $M$ and $N$ respectively, so that $${AM\over AC}={CN\over CE}=r.$$ Determine $r$ if $B,M$ and $N$ are collinear.
Izvor: Međunarodna matematička olimpijada, shortlist 1982
Školjka 
and 
of the regular hexagon 
are divided by inner points 
and 
respectively, so that 
Determine 
if 
and