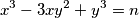
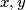
Prove that if is a positive integer such that the equation has a solution in integers , then it has at least three such solutions. Show that the equation has no solutions in integers for .
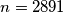
%V0
Prove that if $n$ is a positive integer such that the equation $$x^3-3xy^2+y^3=n$$ has a solution in integers $x,y$, then it has at least three such solutions. Show that the equation has no solutions in integers for $n=2891$.
Izvor: Međunarodna matematička olimpijada, shortlist 1982
Školjka 
is a positive integer such that the equation 
has a solution in integers 
, then it has at least three such solutions. Show that the equation has no solutions in integers for 
.