IMO Shortlist 1983 problem 3
Dodao/la:
arhiva2. travnja 2012. Let

be an equilateral triangle and
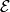
the set of all points contained in the three segments

,

, and

(including

,

, and

). Determine whether, for every partition of
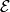
into two disjoint subsets, at least one of the two subsets contains the vertices of a right-angled triangle.
%V0
Let $ABC$ be an equilateral triangle and $\mathcal{E}$ the set of all points contained in the three segments $AB$, $BC$, and $CA$ (including $A$, $B$, and $C$). Determine whether, for every partition of $\mathcal{E}$ into two disjoint subsets, at least one of the two subsets contains the vertices of a right-angled triangle.
Izvor: Međunarodna matematička olimpijada, shortlist 1983