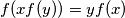
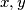
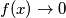
Find all functions defined on the set of positive reals which take positive real values and satisfy: for all ; and as .
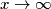
%V0
Find all functions $f$ defined on the set of positive reals which take positive real values and satisfy: $f(xf(y))=yf(x)$ for all $x,y$; and $f(x)\to0$ as $x\to\infty$.
Izvor: Međunarodna matematička olimpijada, shortlist 1983
Školjka 
defined on the set of positive reals which take positive real values and satisfy: 
for all 
; and 
as 
.