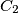
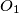
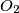
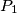
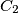
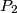
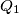
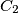
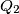
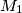
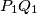
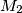
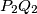
Let be one of the two distinct points of intersection of two unequal coplanar circles and with centers and respectively. One of the common tangents to the circles touches at and at , while the other touches at and at . Let be the midpoint of and the midpoint of . Prove that .
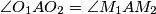
%V0
Let $A$ be one of the two distinct points of intersection of two unequal coplanar circles $C_1$ and $C_2$ with centers $O_1$ and $O_2$ respectively. One of the common tangents to the circles touches $C_1$ at $P_1$ and $C_2$ at $P_2$, while the other touches $C_1$ at $Q_1$ and $C_2$ at $Q_2$. Let $M_1$ be the midpoint of $P_1Q_1$ and $M_2$ the midpoint of $P_2Q_2$. Prove that $\angle O_1AO_2=\angle M_1AM_2$.
Izvor: Međunarodna matematička olimpijada, shortlist 1983
Školjka 
be one of the two distinct points of intersection of two unequal coplanar circles 
and 
with centers 
and 
respectively. One of the common tangents to the circles touches 
and 
, while the other touches 
and 
. Let 
be the midpoint of 
and 
the midpoint of 
. Prove that 
.