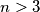
Let be the sum of the lengths of all the diagonals of a plane convex polygon with vertices (where ). Let be its perimeter. Prove that: where denotes the greatest integer not exceeding .
%V0
Let $d$ be the sum of the lengths of all the diagonals of a plane convex polygon with $n$ vertices (where $n>3$). Let $p$ be its perimeter. Prove that:
$$n-3<{2d\over p}<\Bigl[{n\over2}\Bigr]\cdot\Bigl[{n+1\over 2}\Bigr]-2,$$
where $[x]$ denotes the greatest integer not exceeding $x$.
Izvor: Međunarodna matematička olimpijada, shortlist 1984
Školjka 
be the sum of the lengths of all the diagonals of a plane convex polygon with 
vertices (where 
). Let 
be its perimeter. Prove that: ![n-3<{2d\over p}<\Bigl[{n\over2}\Bigr]\cdot\Bigl[{n+1\over 2}\Bigr]-2,](/media/m/b/f/e/bfef9e3a7f90f0997c99d4e834675ae5.png)
![[x]](/media/m/6/a/4/6a47dfb91475b9d5490dbb3a666604a3.png)
denotes the greatest integer not exceeding 
.