IMO Shortlist 1984 problem 8
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Given points  and
and  in the plane. Every point in the plane is colored with one of a finite number of colors. Given a point
in the plane. Every point in the plane is colored with one of a finite number of colors. Given a point  in the plane, the circle
in the plane, the circle 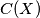 has center
has center  and radius
and radius 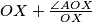 , where
, where 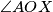 is measured in radians in the range
is measured in radians in the range 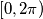 . Prove that we can find a point
. Prove that we can find a point  , not on
, not on 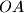 , such that its color appears on the circumference of the circle
, such that its color appears on the circumference of the circle 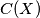 .
.
 and
and  in the plane. Every point in the plane is colored with one of a finite number of colors. Given a point
in the plane. Every point in the plane is colored with one of a finite number of colors. Given a point  in the plane, the circle
in the plane, the circle 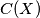 has center
has center  and radius
and radius 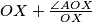 , where
, where 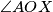 is measured in radians in the range
is measured in radians in the range 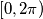 . Prove that we can find a point
. Prove that we can find a point  , not on
, not on 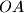 , such that its color appears on the circumference of the circle
, such that its color appears on the circumference of the circle 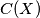 .
. Izvor: Međunarodna matematička olimpijada, shortlist 1984
 Školjka
Školjka 
