IMO Shortlist 1984 problem 12
Dodao/la:
arhiva2. travnja 2012. Find one pair of positive integers
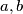
such that
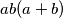
is not divisible by
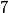
, but
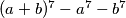
is divisible by
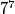
.
%V0
Find one pair of positive integers $a,b$ such that $ab(a+b)$ is not divisible by $7$, but $(a+b)^7-a^7-b^7$ is divisible by $7^7$.
Izvor: Međunarodna matematička olimpijada, shortlist 1984