IMO Shortlist 1985 problem 17
Dodao/la:
arhiva2. travnja 2012. The sequence
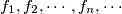
of functions is defined for
recursively by
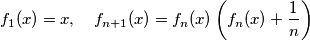
Prove that there exists one and only one positive number

such that
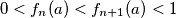
for all integers
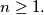
%V0
The sequence $f_1, f_2, \cdots, f_n, \cdots$ of functions is defined for $x > 0$ recursively by
$$f_1(x)=x , \quad f_{n+1}(x) = f_n(x) \left(f_n(x) + \frac 1n \right)$$
Prove that there exists one and only one positive number $a$ such that $0 < f_n(a) < f_{n+1}(a) < 1$ for all integers $n \geq 1.$
Izvor: Međunarodna matematička olimpijada, shortlist 1985