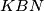
A circle with center passes through the vertices and of the triangle and intersects the segments and again at distinct points and respectively. Let be the point of intersection of the circumcircles of triangles and (apart from ). Prove that .
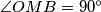
%V0
A circle with center $O$ passes through the vertices $A$ and $C$ of the triangle $ABC$ and intersects the segments $AB$ and $BC$ again at distinct points $K$ and $N$ respectively. Let $M$ be the point of intersection of the circumcircles of triangles $ABC$ and $KBN$ (apart from $B$). Prove that $\angle OMB=90^{\circ}$.
Izvor: Međunarodna matematička olimpijada, shortlist 1985
Školjka 
passes through the vertices 
and 
of the triangle 
and intersects the segments 
and 
again at distinct points 
and 
respectively. Let 
be the point of intersection of the circumcircles of triangles 
(apart from 
). Prove that 
.