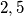
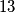
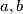
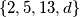
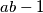
Let be any positive integer not equal to or . Show that one can find distinct in the set such that is not a perfect square.
%V0
Let $d$ be any positive integer not equal to $2, 5$ or $13$. Show that one can find distinct $a,b$ in the set $\{2,5,13,d\}$ such that $ab-1$ is not a perfect square.
Izvor: Međunarodna matematička olimpijada, shortlist 1986
Školjka 
be any positive integer not equal to 
or 
. Show that one can find distinct 
in the set 
such that 
is not a perfect square.