IMO Shortlist 1987 problem 16
Dodao/la:
arhiva2. travnja 2012. Let
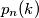
be the number of permutations of the set
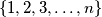
which have exactly

fixed points. Prove that
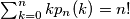
.(IMO Problem 1)
Original formulation
Let

be a set of

elements. We denote the number of all permutations of

that have exactly

fixed points by
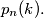
Prove:
(a)
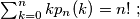
(b)
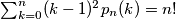
Proposed by Germany, FR
%V0
Let $p_n(k)$ be the number of permutations of the set $\{1,2,3,\ldots,n\}$ which have exactly $k$ fixed points. Prove that $\sum_{k=0}^nk p_n(k)=n!$.(IMO Problem 1)
Original formulation
Let $S$ be a set of $n$ elements. We denote the number of all permutations of $S$ that have exactly $k$ fixed points by $p_n(k).$ Prove:
(a) $\sum_{k=0}^{n} kp_n(k)=n! \ ;$
(b) $\sum_{k=0}^{n} (k-1)^2 p_n(k) =n!$
Proposed by Germany, FR
Izvor: Međunarodna matematička olimpijada, shortlist 1987