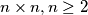
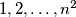
An chessboard is numbered by the numbers (and every number occurs). Prove that there exist two neighbouring (with common edge) squares such that their numbers differ by at least
%V0
An $n \times n, n \geq 2$ chessboard is numbered by the numbers $1, 2, \ldots, n^2$ (and every number occurs). Prove that there exist two neighbouring (with common edge) squares such that their numbers differ by at least $n.$
Izvor: Međunarodna matematička olimpijada, shortlist 1988
Školjka 
chessboard is numbered by the numbers 
(and every number occurs). Prove that there exist two neighbouring (with common edge) squares such that their numbers differ by at least 