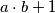
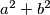
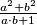
Let and be two positive integers such that divides . Show that is a perfect square.
%V0
Let $a$ and $b$ be two positive integers such that $a \cdot b + 1$ divides $a^{2} + b^{2}$. Show that $\frac {a^{2} + b^{2}}{a \cdot b + 1}$ is a perfect square.
Izvor: Međunarodna matematička olimpijada, shortlist 1988
Školjka 
and 
be two positive integers such that 
divides 
. Show that 
is a perfect square.