IMO Shortlist 1988 problem 26
Dodao/la:
arhiva2. travnja 2012. A function

defined on the positive integers (and taking positive integers values) is given by:
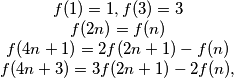
for all positive integers
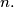
Determine with proof the number of positive integers
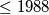
for which
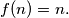
%V0
A function $f$ defined on the positive integers (and taking positive integers values) is given by:
$\begin{matrix} f(1) = 1, f(3) = 3 \\ f(2n) = f(n) \\ f(4n + 1) = 2f(2n + 1) - f(n) \\ f(4n + 3) = 3f(2n + 1) - 2f(n)\text{,} \end{matrix}$
for all positive integers $n.$ Determine with proof the number of positive integers $\leq 1988$ for which $f(n) = n.$
Izvor: Međunarodna matematička olimpijada, shortlist 1988