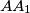
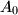
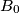
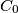
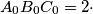
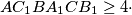
is a triangle, the bisector of angle meets the circumcircle of triangle in , points and are defined similarly. Let meet the lines that bisect the two external angles at and in . Define and similarly. Prove that the area of triangle area of hexagon area of triangle .
%V0
$ABC$ is a triangle, the bisector of angle $A$ meets the circumcircle of triangle $ABC$ in $A_1$, points $B_1$ and $C_1$ are defined similarly. Let $AA_1$ meet the lines that bisect the two external angles at $B$ and $C$ in $A_0$. Define $B_0$ and $C_0$ similarly. Prove that the area of triangle $A_0B_0C_0 = 2 \cdot$ area of hexagon $AC_1BA_1CB_1 \geq 4 \cdot$ area of triangle $ABC$.
Izvor: Međunarodna matematička olimpijada, shortlist 1989
Školjka 
is a triangle, the bisector of angle 
meets the circumcircle of triangle 
, points 
and 
are defined similarly. Let 
meet the lines that bisect the two external angles at 
and 
in 
. Define 
and 
similarly. Prove that the area of triangle 
area of hexagon 
area of triangle