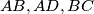
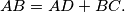
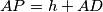
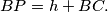
Let be a convex quadrilateral such that the sides satisfy There exists a point inside the quadrilateral at a distance from the line such that and Show that:
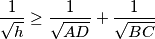
%V0
Let $ABCD$ be a convex quadrilateral such that the sides $AB, AD, BC$ satisfy $AB = AD + BC.$ There exists a point $P$ inside the quadrilateral at a distance $h$ from the line $CD$ such that $AP = h + AD$ and $BP = h + BC.$ Show that:
$$\frac {1}{\sqrt {h}} \geq \frac {1}{\sqrt {AD}} + \frac {1}{\sqrt {BC}}$$
Izvor: Međunarodna matematička olimpijada, shortlist 1989
Školjka 
be a convex quadrilateral such that the sides 
satisfy 
There exists a point 
inside the quadrilateral at a distance 
from the line 
such that 
and 
Show that: 