IMO Shortlist 1990 problem 3
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0 Let  and consider a set
and consider a set  of
of 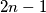 distinct points on a circle. Suppose that exactly
distinct points on a circle. Suppose that exactly  of these points are to be colored black. Such a coloring is good if there is at least one pair of black points such that the interior of one of the arcs between them contains exactly
of these points are to be colored black. Such a coloring is good if there is at least one pair of black points such that the interior of one of the arcs between them contains exactly  points from
points from  . Find the smallest value of
. Find the smallest value of  so that every such coloring of
so that every such coloring of  points of
points of  is good.
is good.
 and consider a set
and consider a set  of
of 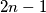 distinct points on a circle. Suppose that exactly
distinct points on a circle. Suppose that exactly  of these points are to be colored black. Such a coloring is good if there is at least one pair of black points such that the interior of one of the arcs between them contains exactly
of these points are to be colored black. Such a coloring is good if there is at least one pair of black points such that the interior of one of the arcs between them contains exactly  points from
points from  . Find the smallest value of
. Find the smallest value of  so that every such coloring of
so that every such coloring of  points of
points of  is good.
is good. Izvor: Međunarodna matematička olimpijada, shortlist 1990
 Školjka
Školjka 
