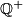
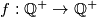
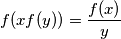
Let be the set of positive rational numbers. Construct a function such that for all , in .
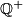
%V0
Let ${\mathbb Q}^ +$ be the set of positive rational numbers. Construct a function $f : {\mathbb Q}^ + \rightarrow {\mathbb Q}^ +$ such that
$$f(xf(y)) = \frac {f(x)}{y}$$
for all $x$, $y$ in ${\mathbb Q}^ +$.
Izvor: Međunarodna matematička olimpijada, shortlist 1990
Školjka 
be the set of positive rational numbers. Construct a function 
such that 
, 
in