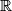
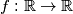
Let denote the set of all real numbers. Find all functions such that
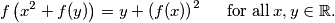
%V0
Let $\,{\mathbb{R}}\,$ denote the set of all real numbers. Find all functions $\,f: {\mathbb{R}}\rightarrow {\mathbb{R}}\,$ such that $$f\left( x^{2}+f(y)\right) =y+\left( f(x)\right) ^{2}\hspace{0.2in}\text{for all}\,x,y\in \mathbb{R}.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1992
Školjka 
denote the set of all real numbers. Find all functions 
such that 