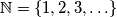
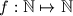
Let . Determine if there exists a strictly increasing function with the following properties:
(i) ;
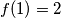
(ii) .
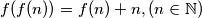
%V0
Let $\mathbb{N} = \{1,2,3, \ldots\}$. Determine if there exists a strictly increasing function $f: \mathbb{N} \mapsto \mathbb{N}$ with the following properties:
(i) $f(1) = 2$;
(ii) $f(f(n)) = f(n) + n, (n \in \mathbb{N})$.
Izvor: Međunarodna matematička olimpijada, shortlist 1993
Školjka 
. Determine if there exists a strictly increasing function 
with the following properties: 
; 
.