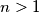
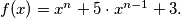
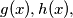
Let be an integer and let Prove that there do not exist polynomials each having integer coefficients and degree at least one, such that
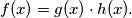
%V0
Let $n > 1$ be an integer and let $f(x) = x^n + 5 \cdot x^{n-1} + 3.$ Prove that there do not exist polynomials $g(x),h(x),$ each having integer coefficients and degree at least one, such that $f(x) = g(x) \cdot h(x).$
Izvor: Međunarodna matematička olimpijada, shortlist 1993
Školjka 
be an integer and let 
Prove that there do not exist polynomials 
each having integer coefficients and degree at least one, such that 