IMO Shortlist 1993 problem C3
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0 Let 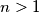 be an integer. In a circular arrangement of
be an integer. In a circular arrangement of  lamps
lamps 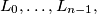 each of of which can either ON or OFF, we start with the situation where all lamps are ON, and then carry out a sequence of steps,
each of of which can either ON or OFF, we start with the situation where all lamps are ON, and then carry out a sequence of steps, 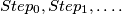 If
If 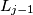 (
( is taken mod
is taken mod  ) is ON then
) is ON then 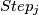 changes the state of
changes the state of 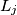 (it goes from ON to OFF or from OFF to ON) but does not change the state of any of the other lamps. If
(it goes from ON to OFF or from OFF to ON) but does not change the state of any of the other lamps. If 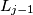 is OFF then
is OFF then 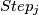 does not change anything at all. Show that:
does not change anything at all. Show that:
(i) There is a positive integer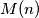 such that after
such that after 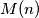 steps all lamps are ON again,
steps all lamps are ON again,
(ii) If has the form
has the form 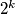 then all the lamps are ON after
then all the lamps are ON after 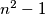 steps,
steps,
(iii) If has the form
has the form 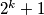 then all lamps are ON after
then all lamps are ON after 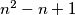 steps.
steps.
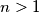 be an integer. In a circular arrangement of
be an integer. In a circular arrangement of  lamps
lamps 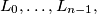 each of of which can either ON or OFF, we start with the situation where all lamps are ON, and then carry out a sequence of steps,
each of of which can either ON or OFF, we start with the situation where all lamps are ON, and then carry out a sequence of steps, 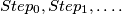 If
If 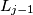 (
( is taken mod
is taken mod  ) is ON then
) is ON then 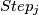 changes the state of
changes the state of 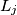 (it goes from ON to OFF or from OFF to ON) but does not change the state of any of the other lamps. If
(it goes from ON to OFF or from OFF to ON) but does not change the state of any of the other lamps. If 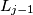 is OFF then
is OFF then 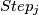 does not change anything at all. Show that:
does not change anything at all. Show that: (i) There is a positive integer
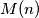 such that after
such that after 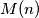 steps all lamps are ON again,
steps all lamps are ON again, (ii) If
 has the form
has the form 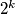 then all the lamps are ON after
then all the lamps are ON after 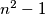 steps,
steps, (iii) If
 has the form
has the form 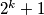 then all lamps are ON after
then all lamps are ON after 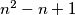 steps.
steps. Izvor: Međunarodna matematička olimpijada, shortlist 1993
 Školjka
Školjka 
